计算机中的P = NP? 问题
在计算机科学领域,有一个悬赏一百万美元的世纪难题,它就是“P=NP?”问题。这个问题非常重要,它关系到计算机的算力极限,也和我们生活中的很多问题(如密码学、物流规划、人工智能等)息息相关。
时间复杂度
在讨论P与NP问题之前,我们需要先简单了解一下时间复杂度,它是衡量一个算法运行效率的标尺。我们通常用大O符号来表示,比如 O(n), O(n²), O(2ⁿ) 等。
常见的算法时间复杂度增长趋势如下: O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)
- 多项式时间复杂度:如 O(1), O(log n), O(n), O(n log n), O(n²), O(n³) 等。它们的特点是,随着问题规模 n 的增长,计算时间的增长速度是可控的。
- 指数时间复杂度:如 O(2ⁿ), O(n!) 等。这类算法的计算时间会随着问题规模 n 的增长而急剧增加,当 n 稍大时,计算就会变得不切实际。
P 问题
P 问题 (Polynomial time) 指的是那些可以在多项式时间内被解决的问题。
简单来说,如果一个问题能找到一个高效的算法,在有限且可接受的时间内计算出结果,那么它就是一个P问题。我们日常遇到的大部分问题,比如排序、查找等,都属于P问题。
NP 问题
NP 问题 (Nondeterministic Polynomial time) 指的是那些可以在多-项式时间内验证一个解是否正确的问题。
注意这里的关键词是“验证”而不是“解决”。NP问题不保证能被快速解决,但如果你给我一个解,我能很快地判断出它是不是正确的解。
一个很经典的例子是“旅行商问题(TSP)”:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并返回起点的最短路径。
- 解决这个问题非常困难,需要尝试大量的可能性。
- 但如果有人给了你一条具体的路径,你可以很容易地计算出总长度,并验证它是否满足某个条件(比如,是否小于1000公里)。
所有的P问题都是NP问题,因为如果一个问题能被快速解决,那么它的解也一定能被快速验证。
NP-Hard 和 NP-Complete
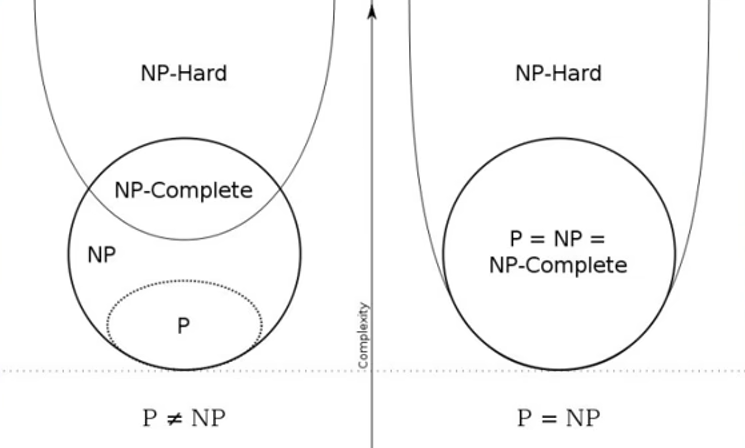
在NP问题中,有一类最难的问题,它们被称为 NP-Complete 和 NP-Hard。
NP-Hard:如果所有的NP问题都能在多项式时间内“归约”到问题 X,那么 X 就是一个 NP-Hard 问题。“归约”可以通俗地理解为“转化”。这意味着 X 问题的难度大于等于任何一个NP问题。它就像是NP世界里的“万恶之源”。
NP-Complete:一个问题既是 NP-Hard 的,同时它本身又是一个 NP 问题,那么它就被称为 NP-Complete 问题。NP-Complete 问题是 NP 问题中最难的一类。
常见的 NP-Complete 问题包括: - 逻辑电路问题 (SAT):给定一个逻辑电路,是否存在一种输入,使其输出为 True。 - 哈密顿回路问题:在一个图中,是否存在一条经过每个顶点一次且仅一次的回路。 - 旅行商问题 (TSP):给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并返回起点的最短路径。
P=NP? 世纪难题
理解了以上概念后,“P=NP?”问题的核心就浮出水面了:
所有能被快速验证解的问题(NP),是否也都存在快速解决它们的算法(P)?
如果 P=NP,意味着所有NP问题(包括所有NP-Complete问题)都能在多项式时间内被解决。这将给科学技术带来革命性的变化:密码学可能被轻易破解,物流和规划问题能找到完美的最优解,人工智能的发展也会迈出一大步。
反之,如果 P≠NP,则意味着存在一类问题,我们能快速验证其解,却无法快速求解。这也符合我们目前的普遍认知。
这个问题在2000年被美国克雷数学研究所列为七个“千年大奖问题”之一,悬赏一百万美元求解。
P与NP的关系图
本文内容部分参考了周扬荣老师的PPT。